Elipso lahko v geometriji ravnine definiramo kot množico točk, tako da je vsota njihovih razdalj do dveh točk (žarišč) konstantna. Tako dobljeno sliko lahko matematično opišemo tudi kot ovalni ali "sploščeni krog". Elipse imajo številne aplikacije v fiziki in so še posebej uporabne pri opisovanju planetarnih orbit. Ekscentričnost je ena od značilnosti in elipse in je merilo, kako krožna je elipsa.
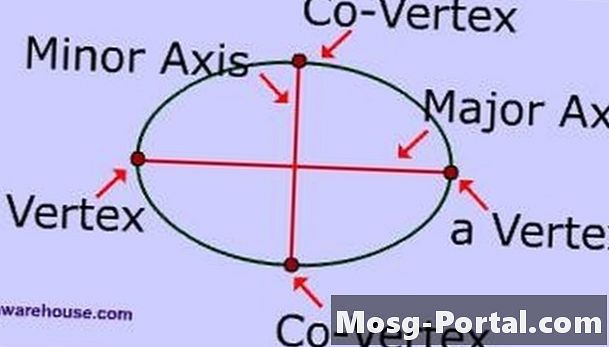
Preglejte dele elipse. Glavna os je najdaljši linijski segment, ki seka središče elipse in ima svoje končne točke na elipsi. Manjša os je najkrajši linijski segment, ki seka središče elipse in ima svoje končne točke na elipsi. Glavna polos je polovica glavne osi, manjša polosna polovica manjše osi.
Preučite formulo elipse. Obstaja veliko različnih načinov opisovanja elipse matematično, najbolj koristen za izračun njene ekscentričnosti pa je za elipso: x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1. Konstante a in b so značilne za določeno elipso, spremenljivki pa sta koordinat točk x in y, ki ležita na elipsi. Ta enačba opisuje elipso s središčem ob izvoru ter glavnimi in manjšimi osmi, ki ležijo na izvorih x in y.
Opredelite dolžine polseki. V enačbi x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1 so dolžine polsil podane z a in b. Večja vrednost predstavlja glavno polosno, manjša vrednost pa manjšo polosno osi.
Izračunajte položaje žarišč. Žarišča so nameščena na glavni osi, ena na vsaki strani središča. Ker osi elipse ležijo na začetnih premicah, bo ena koordinata enaka 0 za obe žarišči. Druga koordinata za bo (a ^ 2 - b ^ 2) ^ (1/2) za eno žarišče in - (a ^ 2 - b ^ 2) ^ (1/2) za druge žarišča, kjer je a> b.
Izračunajte ekscentričnost elipse kot razmerje oddaljenosti žarišča od središča do dolžine pol-glavne osi. Ekscentričnost e je torej (a ^ 2 - b ^ 2) ^ (1/2) / a. Upoštevajte, da je 0 <= e <1 za vse elipse. Ekscentričnost 0 pomeni, da je elipsa krog, dolga tanka elipsa pa ekscentričnost, ki se približa 1.