
Vsebina
Da sta dve obliki skladni, mora imeti vsaka enako število strani, njihovi koti pa morajo biti enaki. Najlažji način za ugotovitev, ali sta dve obliki skladni, je, da eno od oblik zasukate, dokler ni poravnana z drugo, ali preprosto zložite oblike drug na drugega, da ugotovite, ali se kakšni konci držijo. Če oblik ne morete fizično premikati, lahko s pomočjo formul ugotovite, ali so oblike skladne.
Congruent Circles
••• Ray Robert Green / Mediji povpraševanjaVsi krogi imajo enak kot 360 stopinj. Edini dejavnik pri določanju skladnosti dveh krogov je primerjava njihove velikosti. Premer je ravna črta skozi sredino kroga od roba do roba, polmer kroga pa je dolžina od njegovega središča do njegovega zunanjega roba. Z merjenjem katerega koli od obeh v obeh krogih se bo izkazalo, ali sta skladna.
Paralelogrami
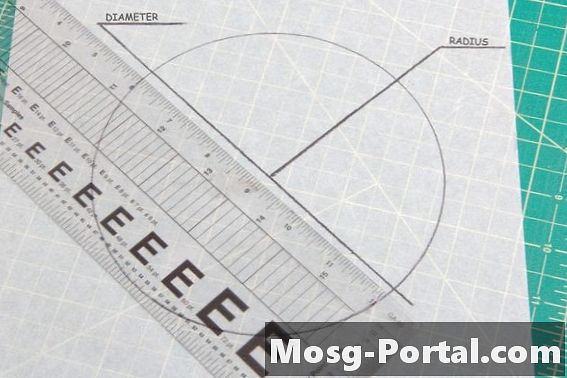
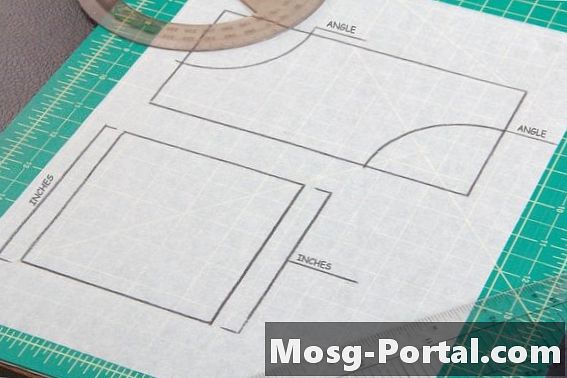
Paralelogram ima dva para vzporednih strani, kot sta kvadrat in pravokotnik. Nasproti strani ali koti paralelograma imajo isto mero, zato je treba na paralelogramu opraviti dve kotni ali stranski meritvi, po eno iz vsakega para strani, da primerjamo skladnost z drugo obliko.
Trikotniki
••• Ray Robert Green / Mediji povpraševanjaČe želite najti skladnost trikotnikov, morate določiti velikost vsakega kota ali strani, saj so lahko vsi trije različni. Obstajajo trije postulati, s katerimi lahko prepoznamo skladne trikotnike. Postulat SSS je, ko v trikotnik izmerite vse tri strani. V postulatu ASA piše, če se kateri koli kot in njuna povezovalna stran ujemata z drugim trikotnikom, potem sta skladna. Postulat SAS deluje nasprotno, saj meri dve strani in njihov povezovalni kot, da se primerja z drugim trikotnikom.
Teoreme za kongruentne trikotnike

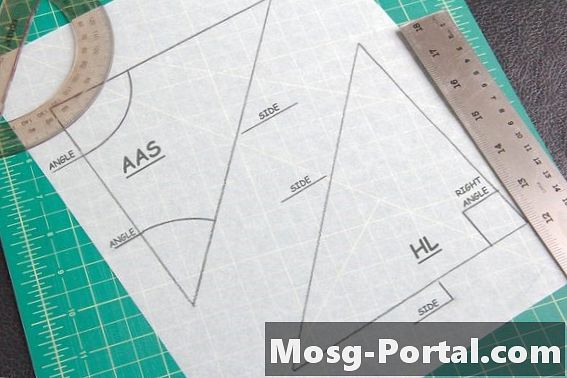
Pri iskanju skladnih trikotnikov sta uporabna dva izrekanja. Teorem AAS pravi, da če sta dva kota in stran, ki ju ne povezujeta, enaka tistemu v drugem trikotniku, potem sta skladna. Teorem Hypotenuse-Leg velja samo za trikotnike z enim 90-stopinjskim ali "pravim" kotom. To je primer, če izmerite hipotenuzo - stran nasproti kota 90 stopinj - in eno od drugih strani trikotnika, da primerjate z drugo obliko.