Vsebina
Vsi desni trikotniki imajo 90-stopinjski ali desni kot. Uporabljajo se v matematiki za posebne izračune, vključno z iskanjem natančne razdalje med dvema točkama. Pravilni trikotniki vam lahko pomagajo tudi pri iskanju višin in razdalj, ki so zelo velike ali drugače težko izmerljive. Pravi trikotniki imajo številne posebne lastnosti, ki so osnova trigonometrije.
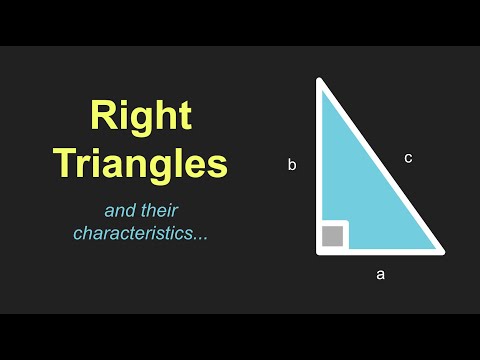
Anatomija desnega trikotnika
Dve krajši strani pravega kota se imenujeta noge. Običajno so označeni s črkama "a" in "b." Tretja stran, ki je nasproti 90-stopinjskemu kotu, se imenuje hipotenuza in je običajno označena s "c."
Pitagorov izrek
Pitagorov izrek pravi, da je vsota dolžine kvadrata desnega trikotnika enaka dolžini kvadrata hipotenuze. Z drugimi besedami, a ^ 2 + b ^ 2 = c ^ 2, kjer sta "a" in "b" noge, "c" pa hipotenuza. Če poznate katero koli stran desnega trikotnika, lahko uporabite teorem in poiščite tretjo stran. To se pogosto uporablja za težko merjenje razdalj ali dolžin. Če na primer veste, da vozite 10 blokov proti jugu, potem 6 blokov proti vzhodu, da pridete od doma do trgovine, vendar želite vedeti, kakšna je neposredna razdalja med domom in trgovino. Lahko bi postavili 10 ^ 2 + 6 ^ 2 = (neposredna razdalja) ^ 2 in ugotovili, da je približno 12 blokov, ko vrana leti.
45-45-90 Trikotniki
Eden izmed posebnih pravih trikotnikov je trikotnik 45-45-90. Nastane z risanjem diagonalne črte od enega vogala do nasprotnega vogala kvadrata. Je edini pravi trikotnik, kjer obe nogi merita natančno enako dolžino. Tako je edini tip pravega trikotnika, ki je tudi enakostelen trikotnik. Ime 45-45-90 izvira iz ukrepov njegovih notranjih kotov. Tu je potreben 90-stopinjski kot, manjši koti pa merijo 45 stopinj. Noge in hipotenuza vedno kažejo razmerje 1: √2. Tako morate za ta trikotnik poznati le dolžino ene strani, da najdete drugi dve dolžini. Dolžine nog so enake, dolžina hipotenuze pa enaka dolžini krat noge √2.
30-60-90 Trikotniki
Tako kot pri trikotniku 45-45-90 tudi trikotnik 30-60-90 dobi ime, ker notranji koti merijo 30, 60 in 90 stopinj. Ta trikotnik je oblikovan tako, da enakomerni trikotnik prerežemo na pol. Strani trikotnikov 30-60-90 tvorijo tudi konstantno razmerje 1: √3: 2. Kratka noga je neposredno čez 30-stopinjski kot in vedno meri polovico dolžine hipotenuze, ki je čez 90-stopinjski kot. Daljša noga, ki je obrnjena od 60-stopinjskega kota, meri dolžino krat kratke noge √3 ali polovico hipotenuznih časov √3. Tako morate za ta trikotnik poznati le dolžino ene strani, da najdete dolžine drugih dveh strani.