Vsebina
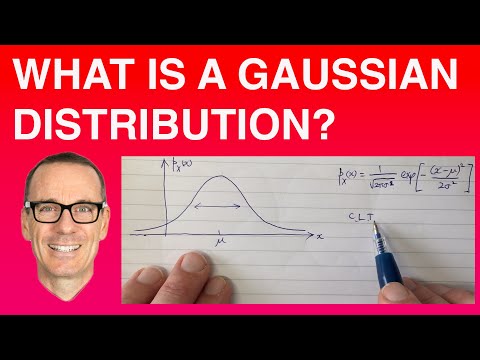
V statistiki se Gaussova ali običajna distribucija uporablja za karakterizacijo zapletenih sistemov z mnogimi dejavniki. Kot je opisano v Zgodovini statistike Stephena Stiglerja, je Abraham De Moivre izumil distribucijo, ki nosi ime Karla Fredricka Gausa. Gausov prispevek je bil v njegovi uporabi razdelitve na najmanjši kvadrat kvadrata za zmanjšanje napak pri prilagajanju podatkov s črto, ki se najbolje prilega. Tako je naredil najpomembnejšo porazdelitev napak v statistiki.
Motivacija
Kakšna je porazdelitev vzorca podatkov? Kaj pa, če ne poznate osnovne podatkovne distribucije? Ali je mogoče preizkusiti hipoteze o podatkih, ne da bi vedeli osnovno distribucijo? Zahvaljujoč teoremu o osrednji meji je odgovor pritrdilen.
Izjava teorema
Navaja, da je povprečna vrednost vzorca iz neskončne populacije približno normalna ali Gaussova, s srednjo vrednostjo kot osnovna populacija in odstopanje, enako odstopanju populacije, deljenem z velikostjo vzorca. Približevanje se izboljša, ko se velikost vzorca poveča.
Približni stavek je včasih napačno naveden kot sklep o konvergenci k normalni porazdelitvi. Ker se približna normalna porazdelitev spreminja, ko se velikost vzorca povečuje, je takšna izjava zavajajoča.
Teorem je razvil Pierre Simon Laplace.
Zakaj je povsod
Normalne porazdelitve so vseprisotne. Razlog izvira iz teoreme o centralni meji. Pogosto, ko se meri vrednost, je učinek vsote mnogih neodvisnih spremenljivk. Zato ima vrednost, ki se meri sama, zanjo kakovost vzorca. Na primer, razporeditev športnih nastopov je lahko zvonasta, kar je posledica razlik v prehrani, treningu, genetiki, trenerstvu in psihologiji. Tudi moška višina ima normalno porazdelitev, saj je odvisna od številnih bioloških dejavnikov.
Gausov Copulas
To, kar se imenuje "funkcija kopule" z Gaussovo distribucijo, je bilo leta 2009 novost zaradi njene uporabe pri ocenjevanju tveganja naložb v zavarovane obveznice. Zloraba funkcije je bila pomembna za finančno krizo 2008–2009. Čeprav je bilo veliko vzrokov za krizo, Gaussove distribucije v zadnjem času verjetno ne bi smeli uporabljati. Funkcija z debelejšim repom bi pripisovala večjo verjetnost neželenim dogodkom.
Izpeljava
Teorem o osrednji meji je mogoče dokazati v številnih vrsticah, če analiziramo funkcijo generiranja trenutka (mgf) (vzorečna srednja - populacijska sredina) /? (Varianta populacije / velikost vzorca) kot funkcija mgf osnovne populacije. Približni del teorema je predstavljen s širitvijo mgf osnovne osnovne populacije kot niz moči, nato pa je prikazano, da je večina izrazov nepomembna, saj se velikost vzorca poveča.
To je mogoče dokazati v veliko manj vrsticah, če uporabimo Taylorjevo razširitev na značilni enačbi iste funkcije in povečamo velikost vzorca.
Računalniška praktičnost
Nekateri statistični modeli domnevajo, da so napake Gaussove. To omogoča distribucijo funkcij normalnih spremenljivk, kot je razdelitev hi-kvadrat in F, pri testiranju hipotez. V F-testu je statistika F sestavljena iz razmerja hi-kvadratnih porazdelitev, ki so same funkcije parametra normalne variance. Razmerje obeh povzroči odstopanje odstopanja, kar omogoča preizkušanje hipotez brez poznavanja odstopanj poleg njihove normalnosti in stalnosti.