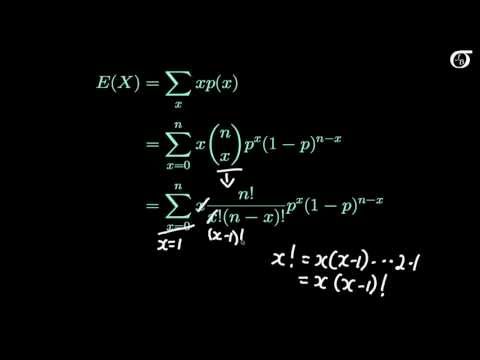
Vsebina
Če 100-krat potegnete matrico in preštejete število krat, ko vržete petico, izvajate binomski eksperiment: 100-krat ponovite metanje matrice, imenovano "n"; Izida sta le dva, bodisi zaviješ petico ali pa ne; in verjetnost, da boste vrgli petico, imenovano "P", je popolnoma enaka vsakič, ko jo zavrtete. Rezultat poskusa se imenuje binomna porazdelitev. Povprečje vam pove, koliko petin lahko pričakujete, da se boste zvrstili, različica pa vam pomaga ugotoviti, kako se lahko vaši dejanski rezultati razlikujejo od pričakovanih rezultatov.
Srednja vrednost binomne porazdelitve
Recimo, da imate v skledi tri zelene marmorje in en rdeči marmor. V svojem poskusu izberete marmor in zapišete "uspeh", če je rdeč ali "neuspeh", če je zelen, in nato postavite marmor nazaj in ponovno izberete. Verjetnost uspeha - izbira rdečega marmorja - je ena od štirih ali 1/4, kar je 0,25. Če bi poskus izvedli 100-krat, bi pričakovali, da narišete rdeči marmor četrtino časa ali skupaj 25-krat. To je srednja vrednost binomne porazdelitve, ki je opredeljena kot število preskusov, 100-krat večja od verjetnosti uspeha za vsako preskušanje, 0,25 ali 100-krat 0,25, kar je enako 25.
Odstopanje binomne porazdelitve
Ko izberete 100 marmorjev, ne boste vedno izbrali točno 25 rdečih marmorjev; vaši dejanski rezultati se bodo razlikovali. Če je verjetnost uspeha "p", je 1/4 ali 0,25, to pomeni, da je verjetnost neuspeha 3/4 ali 0,75, kar je "(1 - p)." Odstopanje je določeno kot število poskusov krat "p" krat "(1-p)." Pri eksperimentu z marmorjem je varianta 100 krat 0,25 krat 0,75 ali 18,75.
Razumevanje variacije
Ker je varianta v kvadratnih enotah, ni tako intuitivna kot srednja. Če pa vzamete kvadratni koren variance, imenovan standardni odklon, vam pove, koliko lahko pričakujete, da se bodo dejanski rezultati v povprečju spreminjali. Kvadratni koren 18,75 je 4,33, kar pomeni, da lahko pričakujete, da bo število rdečih frnikolov med 21 (25 minus 4) in 29 (25 plus 4) na vsakih 100 izbir.