Tangenta je ena od treh osnovnih trigonometričnih funkcij, preostali dve pa sta sinus in kosinus. Te funkcije so ključne za preučevanje trikotnikov in navezujejo kote trikotnika na njegove stranice. Najpreprostejša definicija tangenta uporablja razmerja strani pravega trikotnika, sodobne metode pa to funkcijo izražajo kot vsoto neskončnega niza. Tangenta je mogoče izračunati neposredno, če so dolge stranice desnega trikotnika znane in jih lahko izpeljemo tudi iz drugih trigonometričnih funkcij.
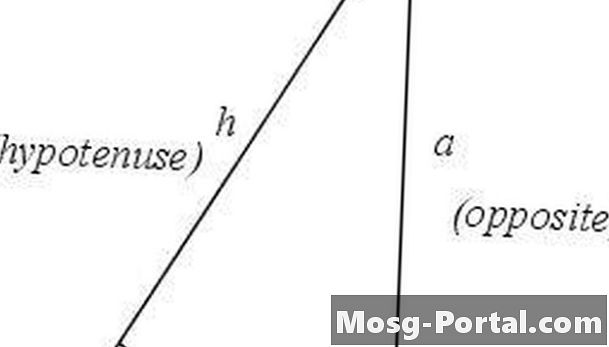
Identificirajte in označite dele pravega trikotnika. Pravi kot bo v zgornjem delu C, stran nasproti njega pa hipotenuza h. Kot θ bo v točki A, preostalo točko pa B. Strani, ki mejijo na kot θ, bodo strani b, stran, nasprotni kot θ, pa bo stran a. Dve strani trikotnika, ki nista hipotenuza, poznamo kot noge trikotnika.
Določite tangento. Tangenta kota je opredeljena kot razmerje med dolžino strani, nasproti kota, in dolžino strani, ki meji na kot. V primeru trikotnika v 1. koraku je tan θ = a / b.
Določite tangento za preprost pravi trikotnik. Na primer, noge enakotničnega desnega trikotnika so enake, zato je a / b = tan θ = 1. Tudi koti so enaki, tako da je θ = 45 stopinj. Zato je porjavelost 45 stopinj = 1.
Izvedite tangento iz drugih trigonometričnih funkcij. Ker je sinus θ = a / h in kosinus θ = b / h, potem je sinus θ / kosinus θ = (a / h) / (b / h) = a / b = tan θ. Zato je tan θ = sinus θ / kosinus θ.
Izračunajte tangento za kateri koli kot in želeno natančnost:
greh x = x - x ^ 3/3! + x ^ 5/5! - x ^ 7/7! + ... kosinus x = 1 - x ^ 2/2! + x ^ 4/4! - x ^ 6/6! + ... Torej tan x = (x - x ^ 3/3! + X ^ 5/5! - x ^ 7/7! + ...) / (1 - x ^ 2/2! + X ^ 4 / 4! - x ^ 6/6! + ...)