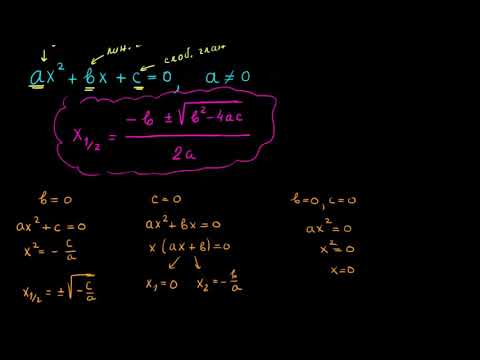
Vsebina
Kvadratna enačba je tista, ki vsebuje eno samo spremenljivko in v kateri je spremenljivka kvadratna. Standardna oblika za to vrsto enačbe, ki vedno tvori parabolo, ko je zgrabljena sekira2 + bx + c = 0, kjer a, b in c so konstante. Iskanje rešitev ni tako preprosto kot za linearno enačbo, del vzroka pa je tudi v tem, da zaradi izraza kvadrata vedno obstajata dve rešitvi. Za reševanje kvadratne enačbe lahko uporabite eno od treh metod. Lahko določite izraze, ki najbolje delujejo s preprostejšimi enačbami ali pa lahko izpolnite kvadrat. Tretja metoda je uporaba kvadratne formule, ki je posplošena rešitev vsake kvadratne enačbe.
Kvadratna formula
Za splošno kvadratno enačbo obrazca sekira2 + bx + c = 0, rešitve so podane s to formulo:
x = ÷ 2_a_
Upoštevajte, da znak ± v oklepaju pomeni, da obstajata vedno dve rešitvi. Ena od rešitev uporablja ÷ 2_a_, druga pa uporablja ÷ 2_a_.
Uporaba kvadratne formule
Preden lahko uporabite kvadratno formulo, se morate prepričati, ali je enačba v standardni obliki. Morda ne bo. Nekateri x2 izrazi so lahko na obeh straneh enačbe, zato jih boste morali zbrati na desni strani. Enako storite z vsemi x izrazi in konstantami.
Primer: Poiščite rešitve enačbe 3_x_2 - 12 = 2_x_ (x -1).
Razširite oklepaje:
3_x_2 - 12 = 2_x_2 - 2_x_
Odštevanje 2_x_2 in z obeh strani. Dodajte 2_x_ na obe strani
3_x_2 - 2_x_2 + 2_x_ - 12 = 2_x_2 -2_x_2 -2_x_ + 2_x_
3_x_2 - 2_x_2 + 2_x_ - 12 = 0
x2 - 2_x_ -12 = 0
Ta enačba je v standardni obliki sekira2 + bx + c = 0 kje a = 1, b = −2 in c = 12
Kvadratna formula je
x = ÷ 2_a_
Od a = 1, b = −2 in c = −12, to postane
x = ÷ 2(1)
x = ÷ 2.
x = ÷ 2
x = ÷ 2
x = 9,21 ÷ 2 in x = −5.21 ÷ 2
x = 4.605 in x = −2.605
Dva drugačna načina reševanja kvadratnih enačb
Kvadratne enačbe lahko rešite s faktoringom. Če želite to narediti, bolj ali manj ugibate na par številk, ki, ko se seštevajo, dajejo konstanto b in ko pomnožimo skupaj, dajemo konstanto c. Ta metoda je lahko težavna, kadar gre za frakcije. in ne bi dobro deloval za zgornji primer.
Druga metoda je izpolniti kvadrat. Če imate enačbo standardni obrazec, sekira2 + bx + c = 0, dal c na desni strani in dodajte izraz (b/2)2 na obe strani. To vam omogoča, da izrazite levo stran kot (x + d)2, kje d je stalnica. Nato lahko vzamete kvadratni koren obeh strani in se odločite za x. Ponovno je enačbo v zgornjem primeru lažje rešiti s kvadratno formulo.