
Vsebina
V geometriji je osmerokotnik poligon z osmimi stranicami. Navadni osmerokotnik ima osem enakih strani in enakih kotov. Navadni osmerokotnik je običajno prepoznaven po znakih zaustavitve. Oktahedron je osemstranski polieder. Navadni oktaedar ima osem trikotnikov z robovi enake dolžine. Učinkovito sta dve kvadratni piramidi, ki se srečujeta na njihovih osnovah.
Formula območja osmerokotnika
Formula za območje pravilnega osmerokotnika s stranicami dolžine "a" je 2 (1 + sqrt (2)) a ^ 2, kjer "sqrt" označuje kvadratni koren.
Izpeljava
Osmerokotnik lahko gledamo kot 4 pravokotnike, en kvadrat v sredini in štiri enakotnike v vogalih.
Kvadrat je površine a ^ 2.
Trikotniki imajo stranice a, a / sqrt (2) in a / sqrt (2) po pitagorejskem izrekanju. Zato ima vsak območje ^ 2/4.
Pravokotniki so površine a * a / sqrt (2).
Vsota teh 9 področij je 2a ^ 2 (1 + sqrt (2)).
Formula volumna oktaedra
Formula volumna pravilnega oktaedra strani "a" je ^ 3 * sqrt (2) / 3.
Izpeljava
Območje štiristranske piramide je območje osnove * višina / 3. Območje pravilnega osmerokotnika je torej 2 * osnova * višina / 3.
Baza = a ^ 2 trivialno.
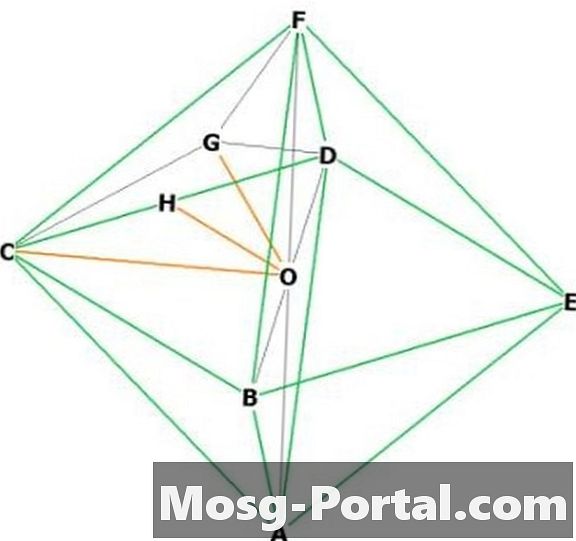
Izberite dve sosednji točki, recimo "F" in "C." "O" je v središču. FOC je enakomerni trikotnik z bazo "a", zato imata OC in OF dolžino a / sqrt (2) po pitagorejevem izrekanju. Torej višina = a / sqrt (2).
Torej je prostornina navadnega oktaedra 2 * (a ^ 2) * a / sqrt (2) / 3 = a ^ 3 * sqrt (2) / 3.
Površina
Navadna površina oktaedrov je območje enakostraničnega trikotnika stranskih "a" krat 8 obrazov.
Če želite uporabiti pitagorejski izrek, spustite črto od vrha do osnove. To ustvari dva prava trikotnika, s hipotenuzo dolžine "a" in ene strani dolžine "a / 2." Zato mora biti tretja stran sqrt = sqrt (3) a / 2. Torej je območje enakostraničnega trikotnika višina * osnova / 2 = sqrt (3) a / 2 * a / 2 = sqrt (3) a ^ 2/4.
Z 8 strani je površina navadnega oktaedra 2 * sqrt (3) * a ^ 2.